In computer science, algorithm is defined as “a finite set of operations for solving a specific type of problem” (Knuth 1997: 3). Basically, algorithms are like recipes, carefully tailored to detail to be followed by novice cooks.
Philosopher of science Daniel Dennett (1995: 50) lists three important characteristics of algorithms:
- substrate-neutrality: the algorithm is a logical structure and can work in many different material instantiations.
- underlying mindlessness: however wonderful the final result may be, each step of the algorithm is tediously simple – simple enough to be carried out without a conscious deliberation.
- guaranteed results: an algorithm always does what it is supposed to do, if all its steps are correctly executed.
To many people, the word ‘evolution’ refers only to the biological evolution. A classical textbook definition of biological evolution is “change, over the course of generations, in the properties of populations of organisms, or groups of populations”; it consists of “descent with modification, and often includes diversification from common ancestors” (Futuyma 1998: 15). However, many biologists, computer scientists, and philosophers prefer today to define evolution as an algorithm, and biological evolution as one of its material instantiations.
Harvard biologist and mathematician Martin Nowak cites replication, mutation, and selection as the three basic building blocks of the algorithm of evolution:
These are the fundamental and defining principles of biological systems. They apply to any biological organization anywhere in our or other universes and do not depend on the particular details of which chemistry was recruited to embody life. (2006: 9)
Oxford zoologist Richard Dawkins, one of the leading figures in theoretical biology, has adopted this view that he dubbed “Universal Darwinism” (1983). Dennett (1995: 343) phrases the same idea in a more generic vocabulary, without reference to biology at all, when he states that evolution occurs whenever the following conditions exist:
- variation: there is a continuing abundance of different elements.
- heredity or replication: the elements have the capacity to create copies or replicas of themselves.
- differential “fitness”: the number of copies of an element that are created in a given time varies, depending on interactions between the features of that element and features of the environment in which it persists.
To express in simpler language, (1) if something is being repeatedly copied (with the copies making further copies of themselves), and (2) if the copying process is not perfect in that sometimes mistakes (variations) occur, and (3) if some sort of selection between different types of copies takes place (i.e. if some of them make more copies of themselves than do the others), evolution just happens. This is the algorithm of evolution; and it is substrate-neutral, mindless, and foolproof. Evolution has absolutely no need for planning or foresight; it is “a scheme for creating Design out of Chaos without the aid of Mind” (Dennett 1995: 50).
The substrate-neutrality of the algorithm is of key importance to the main argument of this thesis. In Susan Blackmore’s words:
A human with a pencil and paper, a hand-cranked adding machine, and a digital computer can all follow the same algorithm for some mathematical procedure and come to the same answer. The substrate does not matter – only the logic of the procedure does. In the case of Darwin’s own argument the substrate was living creatures and a biological environment, but as Dennett points out his logic would apply equally to any system in which there was heredity, variation, and selection. (1999: 11)
To illustrate the point, Figure 1 is an example of the algorithm of evolution working on an imaginary system of populations of replicating orange rounds. [See here for a stand-alone version of this figure, also available in Turkish.]

Figure 1. The algorithm of evolution working on a population of orange rounds.
The example in Figure 1 can also be used to clarify an essential point about evolution which often confuses people: single entities do not evolve. However striking they may be, the changes that an individual thing experiences are not considered evolution (Futuyma 1998: 4). Evolution is a differential and cumulative process working on populations of reproducing entities (Nowak 2006: 9) as seen above.
The fact that this example has a very basic setup designed to illustrate the three conditions of the algorithm of evolution may lead to a popular misunderstanding which can be summed up by the phrase “to complete the evolution”. In fact, evolution is not something that can be completed. (Except for some idealized cases of digital evolutionary algorithms; see section 4.4.) It is not a linear progress towards a specific long-distance goal, or an ideal ‘perfect’ design. Three facts help clarify this truth: (1) the environment of an evolving system, thus the selection pressures acting upon it, hardly stay the same; (2) there usually are multiple alternative solutions to a problem; (3) the ‘necessary’ mutations for a type of solution may not always arise. (Dawkins 1986: 21–193) Evolution is a process of elimination (‘evolution-away-from’) rather than a process of progression (‘evolution-toward’) (Bradford & Dill 2007).
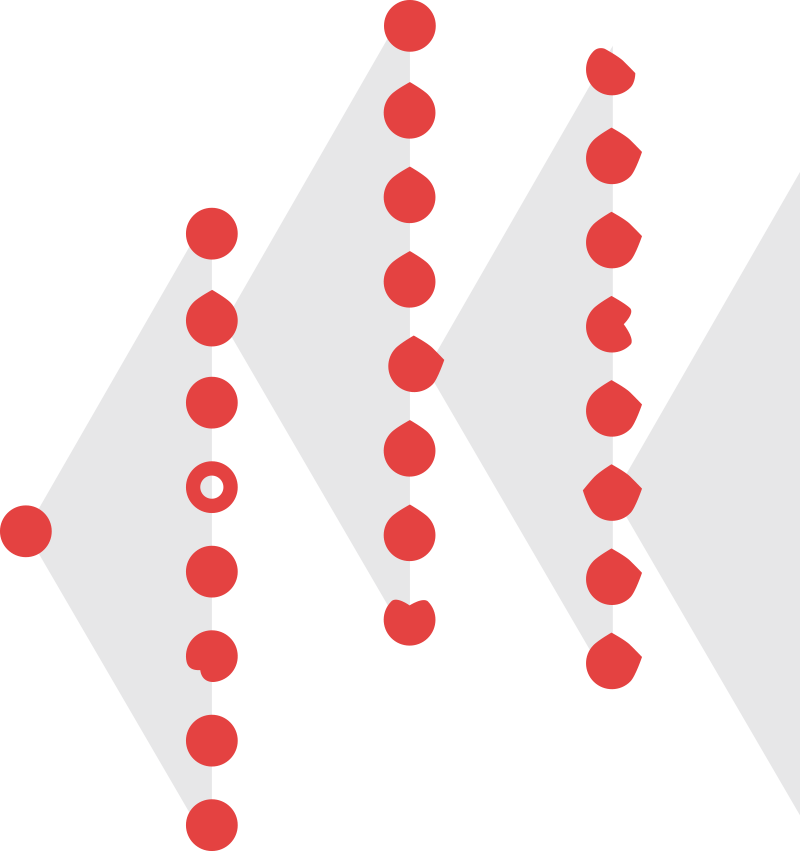
Figure 2. A possible evolutionary history of the population of orange rounds.